Tupper’s self-referential formula #whoa

By ,

Learning about this has made my brain quietly implode.

“Tupper’s self-referential formula is a self-referential formula defined by Jeff Tupper that, when graphed in two dimensions, can visually reproduce the formula itself. It is used in various math and computer science courses as an exercise in graphing formulae.

Specifically (From Wikipedia):

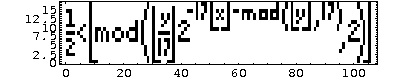
The formula is an inequality defined by:

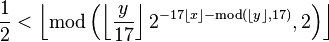
{1\over 2} < \left\lfloor \mathrm{mod}\left(\left\lfloor {y \over 17} \right\rfloor 2^{-17 \lfloor x \rfloor - \mathrm{mod}(\lfloor y\rfloor, 17)},2\right)\right\rfloor

where \lfloor \cdot \rfloor denotes the floor function and mod is the modulo operation.

Let k equal the following:

48584506361897134235820959624942020445814005879832445494830930850619347047088099284506447698655243648499972470249151191
104116057391774078569197543265718554420572104457358836818298237541396343382251994521916512843483329051311931999535024137
58765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586
052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929
001765967965480064427829131488548259914721248506352686630476300

If one graphs the set of points (x,y-k) with 0 \le x \le 106 and k \le y \le k + 17 such that they satisfy the inequality given above, the resulting graph looks like this:

Related Topics

terryman

David (@ng_dave) is Faculty at the Michael Smith Labs. His writing has appeared in places such as McSweeney's, The Walrus, and boingboing.net. He plans on using Terry as another place to highlight the mostly science-y links he appreciates. In fact, if you liked this one, you might also like his main site generally - this can be found at popperfont.net.